100. 相同的树

题目描述

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1： ex1

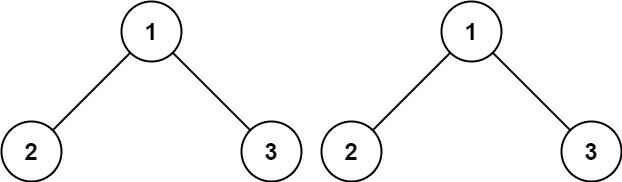
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2： ex2

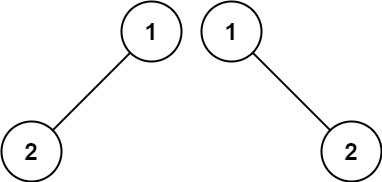
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3： ex3

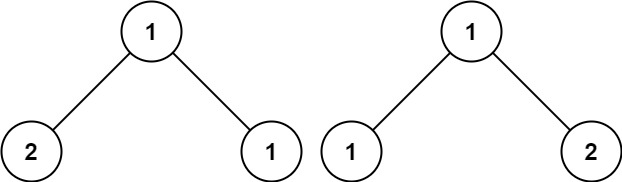
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-104 <= Node.val <= 104

解题方法

方法一：dfs

思路：
- 深度优先遍历
步骤：
- 判断两棵树节点
  - 都为空则相同
  - 一个为空另一个不为空，不同
  - 节点都有值但是 val 不同，不同
  - 递归他们的左子树和右子树
复杂度分析：
- 时间复杂度：O(n)，n 为树节点个数
- 空间复杂度：O(n)，递归层数，即高度较小二叉树的高度

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
  if (p === null && q === null) {
    return true;
  }
  if (p === null || q === null) {
    return false;
  }
  if (p.val !== q.val) {
    return false;
  }
  return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

方法二：bfs

思路：
- 广度优先遍历，判断树结构是否相同，再判断值是否相同
步骤：
- 创建队列存储二叉树每一层的节点，每次取队头进行比较
  - 若两个节点值不同则不同
  - 若值相同，判断两个左右子节点是否为空，如果只有一个为空则结构不同
  - 若两左右子节点结构相同，将非空节点加入队列
复杂度分析：
- 时间复杂度：O(n)，二叉树节点数
- 空间复杂度：O(n)，二叉树节点数

队列可以使用对象的形式，只创建一个就 OK，很巧妙

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
  if (p === null && q === null) {
    return true;
  } else if (p === null || q === null) {
    return false;
  }
  const queue = [{ p, q }];
  while (queue.length) {
    const cur = queue.shift();
    if (cur.p === null && cur.q === null) {
      continue;
    }
    if (cur.p === null || cur.q === null) {
      return false;
    }
    if (cur.p.val !== cur.q.val) {
      return false;
    }
    queue.push({ p: cur.p.left, q: cur.q.left });
    queue.push({ p: cur.p.right, q: cur.q.right });
  }
  return true;
};

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {boolean}
 */
var isSameTree = function (p, q) {
  if (p === null && q === null) {
    return true;
  } else if (p === null || q === null) {
    return false;
  }
  const queue1 = [p];
  const queue2 = [q];
  while (queue1.length && queue2.length) {
    const n1 = queue1.shift();
    const n2 = queue2.shift();
    const left1 = n1.left;
    const left2 = n2.left;
    const right1 = n1.right;
    const right2 = n2.right;
    if (n1.val !== n2.val) {
      return false;
    }
    if ((left1 === null) ^ (left2 === null)) {
      return false;
    }
    if ((right1 === null) ^ (right2 === null)) {
      return false;
    }
    if (left1) {
      queue1.push(left1);
    }
    if (left2) {
      queue2.push(left2);
    }
    if (right1) {
      queue1.push(right1);
    }
    if (right2) {
      queue2.push(right2);
    }
  }
  return queue1.length === 0 && queue2.length === 0;
};

题目描述​

解题方法​

方法一：dfs​

方法二：bfs​

题目描述

解题方法

方法一：dfs

方法二：bfs